
Here's an unusual envelope fold that demonstrates a couple of mathematical points relating to triangles.
Maths is not my strong suit, but I can see that the mathematical aspects of this design are probably more interesting than the envelope itself, because as an envelope it's not really very secure or practical (there are plenty of much better envelope folds out there). However, the folding sequence is quite interesting, and if you seal the flaps with a little sticker at the end it might be good for sending notes to mathematically minded friends.
Paper Protractor
It all started with a Paper Protractor which I found on Arvind Gupta's Toys from Trash website. Wikipedia tells me that Arvind Gupta is an Indian science educator known for developing simple science teaching aids and toys from readily available materials, and his website has plenty of ideas that are worth investigating. With the Paper Protractor, a square with four folds gives you a protractor having angles of 15°, 30°, 45°, 60°, 75°, 90°, 120° and 135°. It's not credited to anyone in particular, so I assume it's by Arvind Gupta, although there are other things on the site that are not credited and yet are definitely attributable to other people.
Internal angles of a triangle always add up to 180°
The other mathematical part of the Triangulope is something I first saw this in Martin Gardner's Encyclopedia of Impromptu Magic (1978), where he calls it a "a dramatic proof that the sum of the angles of a triangle is equal to a straight angle". It seems this was one of the additions made when the encyclopedia was published in book form by Magic Inc., as the item is not included in the original series of articles in Hugard's Magic Monthly magazine. Gardner traces it back to Geometrical Exercises in Paper Folding (1901) by T. Sundara Row (page 90 of the first edition, available online here), which refers to "the property that the three interior angles of a triangle are together equal to two right angles". But it has appeared in various other places, the oldest of which seems to be La science amusante (1890) by Tom Tit (Arthur Good). See How to Sum the Angles of a Triangle in David Mitchell's Public Paperfolding History Project for details of a number of other sources.
 | 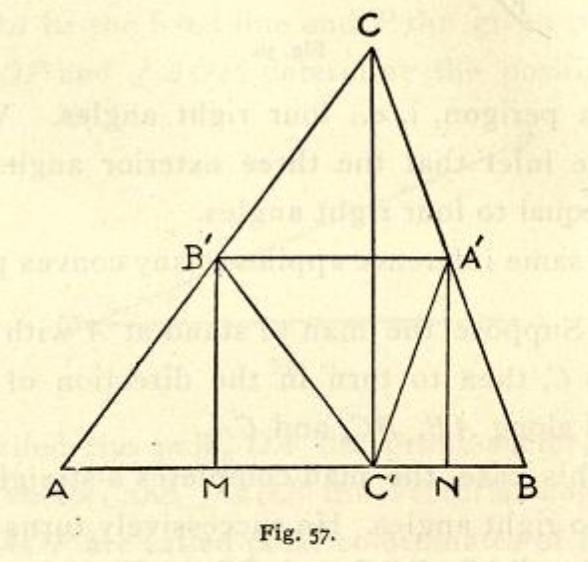 |
Encyclopedia of Impromptu Magic by Martin Gardner | Geometrical Exercises in Paper Folding by T. Sundara Row |
Triangulope
Combining these two ideas I came up with the Triangulope. As already mentioned, it's not really very secure, but the same is true of quite a lot of origami envelopes.
For the summing of internal angles demonstration to work, one of the points or corners has to be brought down to make a fold which is parallel to the bottom edge. In the method diagrammed it's the 45° corner, though it can be any of the three. I did try with the other two but it was difficult to come up with decent envelopes. Something that might be worth experimenting with, perhaps.
I also have a Squarevelope, a Pentalope and a Hexalope, which are a different in that the final forms are a square, pentagon and hexagon respectively. All I need now to complete the set - if I can work out what they would look like - are a Onevelope and a Twovelope.
Comments